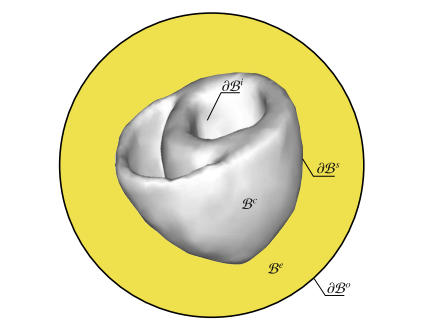
Computational Cardiology
This contribution presents a novel three-dimensional constitutive model which describes the orthotropic electro-visco-elastic response of the myocardium. The model can be regarded as the viscoelastic extension of the recently proposed generalized Hill model for orthotropic active muscle cells. The formulation extends the recent contributions of Cansız et al. (CMBBE 18: 1160–1172, 2015) and Göktepe et al. (JMPS 72: 20–39, 2014) in a novel rheological description which incorporates the active (electrical) and mechanical (viscous and elastic) deformations in a multiplicative format. To this end, the stress response is additively decomposed into passive (purely mechanical) and visco-active (electro-visco-elastic) contributions in line with a rheological model in which the passive part is connected parallel to a branch that consists of an elastic spring, a dashpot and a contractile element in serial. The former branch is assumed to be a function of the total deformation gradient while the formulation of the latter one is based on a multiplicative decomposition of the total deformation gradient into a mechanical and an active part. The active deformation gradient is devised by means of the prescribed active stretch which arises from the electrical excitation of the myocardial tissue and is governed by the intracellular calcium concentration. Thanks to the proposed rheology, marked differences are observed in isometric and isotonic tests between viscoelastic and elastic cases that are performed on material level. Moreover, novel evolution equations for the description of active stretch and intracellular calcium concentration having superiorities over the existing approaches have been proposed.
Collaborators:
Bariş Cansız, Serdar Göktepe, Ellen Kuhl, Michael Kaliske
Recent Publications:
- Cansiz, B. ; Dal, H.; Kaliske, M. [2017]: Computational cardiology: A modified Hill model to describe the electro-visco-elasticity of the myocardium. Computer Methods in Applied Mechanics and Engineering 315, 434–466.
- Can Cansız, F. B.; Dal, H.; Kaliske, M. [2015]: An orthotropic viscoelastic material model for passive myocardium: Theory and algorithmic treatment. Computer Methods in Biomechanics and Biomedical Engineering 18, 1160–1172.
- Corrigendum to'An orthotropic viscoelastic material model for passive myocardium: theory and algorithmic treatment'.
FB Cansız, H Dal, M KaliskeComputer methods in biomechanics and biomedical engineering 19 (1), iii
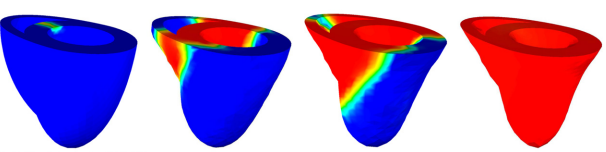
Computational Multi-physics Models for Lithium-Ion Batteries
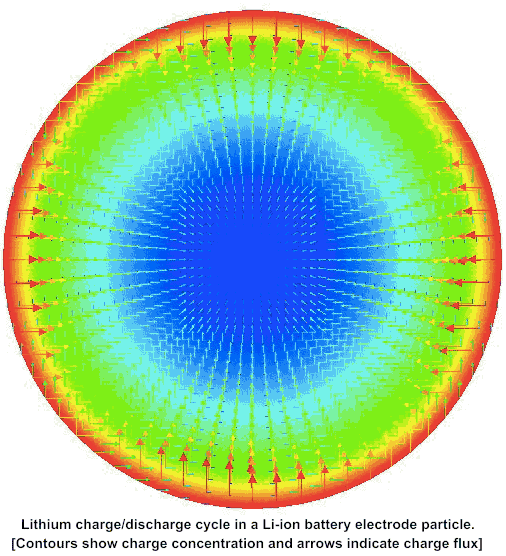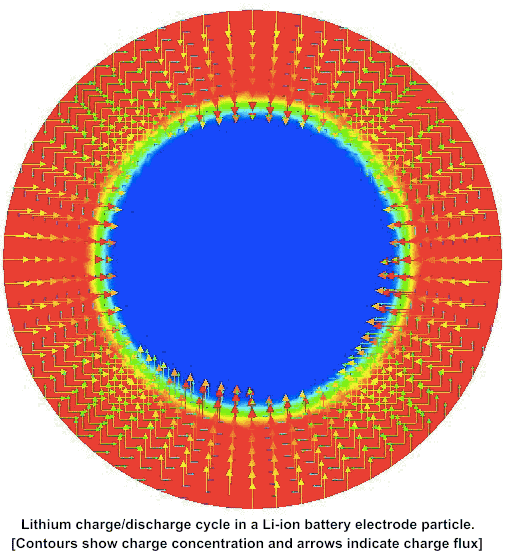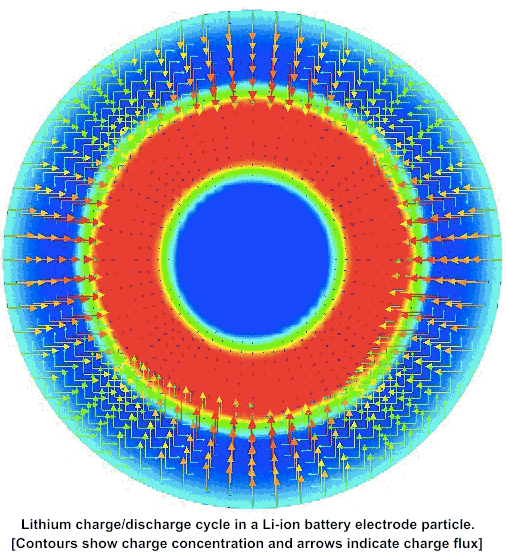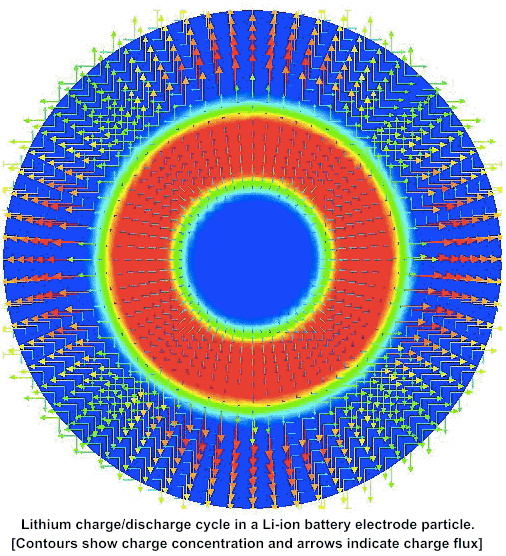
Capacity fade in conventional Li-ion battery systems due to chemo-mechanical degradation during charge–discharge cycles is the bottleneck in high-performance battery design. Stresses generated by diffusion-mechanical coupling in Li-ion intercalation and deintercalation cycles, accompanied by swelling and shrinking at finite strains, cause micro-cracks, which finally disturb the electrical conductivity and isolate the electrode particles. This leads to battery capacity fade. As a first attempt towards a reliable description of this complex phenomenon, we propose a novel finite strain theory for chemo-elasticity coupled with phase-field modeling of fracture, which regularizes a sharp crack topology. We apply a rigorous geometric approach to the diffusive crack modeling based on the introduction of a global evolution equation of regularized crack surface, governed by the crack phase field. The irreversible evolution of the crack phase field is modeled through a novel critical stress-based growth function. A modular concept is outlined for linking of the diffusive crack modeling to the complex chemo-elastic material response of the bulk material. Here, we incorporate standard as well as gradient-extended Cahn–Hilliard-type diffusion for the Li-ions, where the latter accounts for a possible phase segregation. From the viewpoint of the methodology, the separation of modules for the crack evolution and the bulk response provides a highly attractive and transparent structure of the multi-physics problem. This structure is exploited on the numerical side by constructing a robust finite element method, based on an algorithmic decoupling of updates for the crack phase field and the state variables of the chemo-mechanical bulk response. We demonstrate the performance of the proposed coupled multi-field formulation by an analysis of representative boundary value problems.
Collaborators:
Christian Miehe
Recent Publications:
- A phase‐field model for chemo‐mechanical induced fracture in lithium‐ion battery electrode particles
C Miehe, H Dal, LM Schänzel, A RainaInternational Journal for Numerical Methods in Engineering - Computational electro-chemo-mechanics of lithium-ion battery electrodes at finite strains
H Dal, C MieheComputational Mechanics, 1-23
Phase Field Models for the Failure in Anisotropic Continua
Rubbery polymers are subjected to severe environmental conditions under service. As a consequence of various ageing mechanisms, the outer surface of rubber components hardens in time and cracking occurs as a result of combined mechanical and chemical processes. Conventional phenomenological hyperelastic constitutive models do not account for material softening. Consequently, the stored energy and stresses tend to infinity as stretch increases. In this contribution, a network alteration for the ageing mechanism of rubber-like materials is introduced along with a micromolecular description of material failure. The proposed micro-continuum material model is based on a serial construction of a Langevin-type spring representing the energy storage owing to conformational changes induced by deformation, to a bond potential representing the energy stored in the polymer chain due to the interatomic displacement. For the representation of the micro–macro transition, the non-affine kinematics of the micro-sphere model is used. The Morse potential is utilized for the interatomic bond, which describes the energetic contribution to rubber-like materials and governs the failure of the polymer chain in terms of bond rupture. A novel numerical scheme for the FE implementation of the proposed model is demonstrated. The hardening phenomenon as a result of diffusion limited oxidation of rubber is explained by the principle of mass conservation which dictates simultaneous modulus hardening along with decrease in ultimate stretch observed in aged rubbery polymers.
Collaborators:
Gerhard Holzapfel, Osman Gültekin
Recent Publications:
- Gultekin, O. ; Dal, H.; Holzapfel, G.A. [2016]: A phase-field approach to model fracture of arterial walls: Theory and finite element analysis. Computer Methods in Applied Mechanics and Engineering 312, 542–566.
- Coupled chemomechanics and phase field modeling of failure in electrode materials of Li‐ion batteries
H Dal, C MiehePAMM 13 (1), 207-208 - Schanzel, L.M.; Dal, H.; Miehe, C. [2013]: Phase field modeling of fracture in rubbery polymers. Constitutive Models for Rubber VIII, 335-341
- Phase field modeling of fracture in rubbery polymers
L Schanzel, H Dal, C MieheConstitutive Models for Rubber VIII, Taylor & Francis Group, London, 335-341 - A Phase-Field Approach to Model Fracture of Arterial Walls
O Gültekin, H Dal, GA Holzapfel